목표
- 예제를 통해 로지스틱 회귀를 이해한다.
- 시그모이드함수를 이해한다.
- 분류문제 사례를 보고 '이진 클래스 분류'와 '멀티 클래스 분류' 문제 해결 방법을 이해한다.
6. Logistic Regression
이전 강의에서 선형회귀를 이용하여 연속된 함수를 예측해보았다. 주택크기에 따른 집값과 같이 특징(주택크기)과 결과값(집값)이 관계가 있기때문에 연속된 함수로 최적의 가설을 뽑아내는 것이 가능했다.
하지만 연속한 함수로 해결되지 않는 즉, 연속하지 않는 데이터를 학습할때 Logistic Regression을 이용한다.
6.1. Classification
Classification은 이산값을 갖는 데이터를 말한다. 이산은 Discrete로 '별개의'라는 의미를 갖는다. 한자해석으로는 '떨어져 흝어짐' 즉, 이산적인 수학 구조는 연속되지 않는 공간을 다루는 학문이다. Classifcation문제를 갖는 데이터를 Logistic Regression을 통해 해결할수 있을것이다.
분류 문제의 대한 사례를 보자
- 스팸 이메일인가? 아닌가?
- 종양이 양성인가? 악성인가?
위 문제를 도식화하면 연속한 데이터가 아닌 이분화된 데이터를 갖을 것이다. 이때 새로운 데이터가 입력됐을때, 어디로 분류할 것인지에 대한 문제이다. 즉 0또는 1의 값을 갖는 종속변수 y를 예측하는 것이다. 양성이다=1, 악성이다=0과 같이 결과값에 class(negative class, positive class)를 부여한다. 우선 두가지 클래스 분류를 다루고 이후에 0,1,2..,n값을 갖는 멀티클래스 문제를 다룬다. 0과 1을 나누는 원리로 멀티클래스 문제도 해결한다.

연속하지 않은 데이터에 선형회귀를 적용한다면 ?
아래는 종양의 크기에 따라 악성(1), 양성(0)을 표시한 데이터이다. 왼쪽이미지를 보자. 선형회귀를 이용하여 분홍색 직선을 그은후 y축의 0과 1 사이인 0.5에 선을 그어본다. 이때 x축의 임계점을 기준으로 분류가 잘 되어있다. 하지만 데이터들은 이렇게 친절하지 않다. 오른쪽 이미지 처럼 매우 큰 종양이 있을수 있다. 그렇다면 선형회귀의 직선은 더 완만해지고 임계점은 우측으로 이동할 것이다. 왼쪽 이미지와 달리 산개한 데이터를 선형회귀로 학습하면 비정상적인 데이터가 된다.

6.2. Logistic Regression : Hypothesis(Sigmoid)
분류문제일때 가설함수는 로지스틱함수를 사용한다. 로지스틱함수는 시그모이드 함수라고도 부른다. 시그모이드는 0이나 1에 근접할때 까지 천천히 변화하다가, 0과 1 근처에서 평평하게 수렴한다. 예를들어 종양 분류 가설h(θ)의 출력값이 0.7이다. 그렇다면 y=1일 확률이 70%라는 의미이다.

6.3. Logistic Regression : Decision Boundary
결정경계란 분류를 하기 위한 임계선이다. 아직 가설을 최적화하는 방법을 배우진 않았지만, 데이터에 최적화된 가설이 완성된다면 아래와 같은 직선이 될 것이다. 이것이 Decision Boundary(결정 경계)이다.
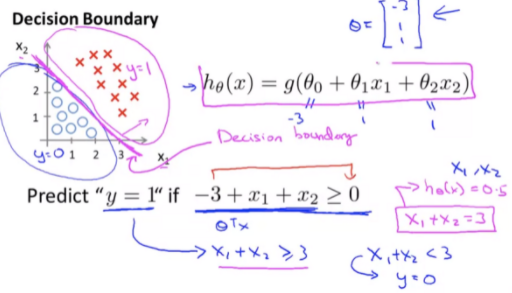
클래스가 두개일때 결정경계를 만드는 방법은 다양하다. 시그모이드 함수에 고차 다항식 항을 대입하면 복잡한 경계를 만들수도 있다.

결정경계를 결정짓는 함수가 시그모이드 함수이다. 0.5를 기준으로 y가1, y=0을 판단 할수 있기 때문에 결정경계를 나누기 최적의 함수가 된다.
- (y = 1) g(z) >= 0.5 == z >= 0 == θ^T * X >= 0
- (y = 0) g(z) < 0.5 == z < 0 == θ^T * X < 0

6.4. Logistic Regression : Cost Function
로지스틱 회귀의 비용함수는 선형회귀 비용함수를 변형하여 사용한다. 그 이유는 선형회귀의 비용함수를 그대로 사용하여 경사하강법을 진행했을때 연속한 데이터를 갖지 않기 때문에 비선형의 울퉁불퉁한 그래프를 나타낸다. 때문에 선형회귀에 적용한 경사하강법을 사용하게 되면 최적의 가설을 찾을 수 없게 된다.

파란색 선형회귀 비용함수 부분을 빨간색 로지스틱회귀 비용함수로 재정의한다.

비용함수cost는 아래와 같다. 복잡한 함수같지만 도식화된 그래프를보면 이해할수 있다. log안의 가설h는 시그모이드 함수이므로 0~1의 값만 고려하면된다. 또한 시그모이드 값 y=1일때 비용함수가 0인 것을 알수있다. 정리해보면 아래와 같다.
- y가 1일때 h=1 이면 일치하여 비용은 0이다.
- y가 1일때 h=0 이면 일치하지 않았으므로 비용은 무한대이다.
- y가 0일때 h=0 이면 일치하여 비용은 0이다.
- y가 0일때 h=1 이면 일치하지 않았으므로 비용은 무한대이다.
일치했을때 비용이 발생하지 않고, 일치하지 않았을때 비용이 발생한다.

6.5. Logistic Regression : Simplified Cost Function and Gradient D
비용함수Cost(hθ(x), y)에서 y는 항상 1또는 0의 값만 갖기 때문에 수학적으로 정리하여 한줄의 방정식으로 표현이 가능하다.

비용함수가 완성됐으므로 경사하강법을 통해 최적화를 하면된다.
경사하강법에 대한 설명은 간략하다. 그 이유는 전 게시물에서 원리를 설명한 바가 있다. 하지만 그뿐아니라 경사하강법과 같은 최적화 알고리즘 라이브러리가 오픈소스로 제공된다. 결론은 고급 최적화 알고리즘은 구현할 필요없으며, 라이브러리의 사용법을 익히고 사용만 하면된다.
6.6. Logistic Regression : Multiclass Classification
멀티클래스 분류 사례가 무엇이 있으며 어떻게 해결할까?
- 날씨 분류 : 맑음, 흐림, 비, 눈 (0, 1, 2, 3)
- 코막힘 진단 분류 : 건강, 감기, 독감 (0, 1, 2)
세가지 이상의 클래스를 갖는 분류문제이다. 이진분류 문제와 멀티클래스 분류문제를 비교하며 이해해본다. 이진분류문제는 그룹사이를 결정경계로 나누어 positive class와 negative class로 나누었다. 멀티클래스 분류 문제도 이진분류 문제로 생각할수 있다. 3가지 클래스가 있다면 가설에 인덱스를 부여하고 3개의 가설을 세우면된다. △에 대한 가설을 세울때 △이외의 데이터를 모두 ㅇ데이터로 치환하고 △는 positive, ㅇ는 negative 클래스로 분류 하면된다. 즉, 여러 클래스가 있을때 한 클래스 관점에서 다른 클래스를 negative로 치환하여 이진분류문제처럼 해결하는 것이다.

위와 같은 방법으로 3개의 클래스에 대해 3개의 가설을 세울수 있다. 새로운 입력값x을 예측할때는 3개의 가설함수에 값을 대입해 본다. 그럼 제일 높은 확률의 클래스가 나올것이므로 입력값x는 해당 클래스로 분류될 수 있다.

참조
머신러닝 코세라 : https://ko.coursera.org/learn/machine-learning
라인하트 브런치 : https://brunch.co.kr/@linecard
'머신러닝' 카테고리의 다른 글
| [머신러닝 이론] 8. Neural Networks(신경망) 1 - 앤드류응 강의 (0) | 2022.06.25 |
|---|---|
| [머신러닝 이론] 7. Regularization(정규화) - 앤드류응 강의 (0) | 2022.06.02 |
| [머신러닝 이론] 5. Octabe/Matlab 튜토리얼 - 앤드류응 강의 (0) | 2022.05.28 |
| [머신러닝 이론] 4. 다변수 선형회귀 - 앤드류응 강의 (0) | 2022.05.15 |
| [머신러닝 이론] 3. 머신러닝에 필요한 선형대수 복습 - 앤드류응 강의 (0) | 2022.05.15 |


