순서가 있는 게시물 입니다.
[머신러닝 이론] 2. 단변수 선형회귀(1) - 앤드류응 강의
[머신러닝 이론] 2. 단변수 선형회귀(2) - 앤드류응 강의
목표
- 예제를 통해 단변수 선형회귀(Linear Regression with One Variable)를 이해한다.
- 비용함수(Cost Function)과 경사하강법(Gradient Descent)를 이해한다.
2. Linear Regression with One Variable
2.1. Model and Hypothesis
가설의 예시를 보자.
집값과 평수 데이터를 도식화하였다. 그리고 데이터셋에 대략적으로 일치하는 직선(가설)을 그었다. 그리고 나의 집의 평수를 초록색으로 표현하여 비교를 해보았다. 평수로 나의 집값을 얼추 짐작할 수 있게됐다.
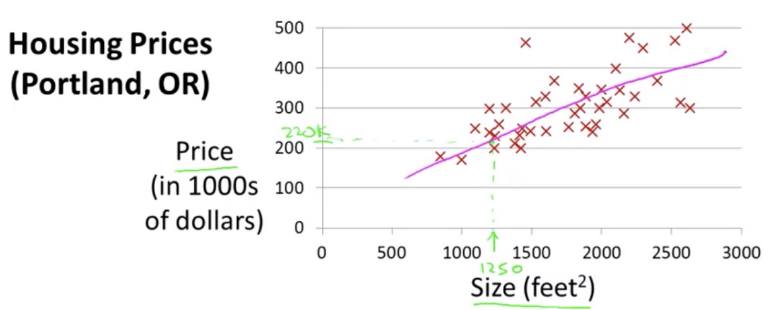
위의 내용이 지도학습의 사례이다. 학습데이터에 정답이 있고 그 데이터를 바탕으로 집값을 예측하는 가설을 세워 선형회귀적 학습을 했기 때문이다.
위의 예시로 용어 및 표기법을 정의해본다.
- Data set : Training set (평수와 집값을 갖은 데이터)
- m : 데이터의 row수(데이터의 개수)
- i : 데이터의 순번
- x : feature를 나타내는 입력변수(평수)
- y : 출력값 또는 예측하기 위한 목표변수(집값)
- (x^(i), y^(i)) : i 번째 데이터, 예) x^(2) = 1416

그래서 머신러닝에서 가설이 뭔데 ?
아래 그림과 같이 학습 알고리즘(Learning Algorithm)에 데이터셋(Traning Set)을 넣고 학습시키면 학습알고리즘은 가설(h, hypothesis)을 제시한다. 이때 h함수는 데이터셋에 존재하지 않는 새로운 데이터를 넣었을때 적절한 결과를 제시해 준다.
이전에 평수 대비 집값 데이터로 선형함수를 그렸다 .이 직선은 가설이자 방정식이며 hθ(x) = θ0 + θ1x 이다.
가설 부가설명 - 매개변수θ가 무엇인가
어렵게 생각하지 않아도 된다. 흔히 아는 y=ax+b라는 1차 방정식은 직선을 나타낸다. 이때 직선의 모양을 결정하는 값 a,b가 θ0, θ1로 치환됐다고 생각하면 된다. 더 나가아 단변수 선형회귀의 목적은 데이터에 적합한 직선을 찾는것이며 직선의 모양을 결정하는 파라미터 θ0, θ1을 찾는 것이다.

2.2. Cost Function
Cost Function(비용함수)이란 학습데이터와 오차가 가장 작은 가설함수를 찾기 위한 함수이다. 비용함수를 통해 데이터에 가장 적합한 직선을 찾아 낼수 있을것이다.
Loss Function과 Cost Function을 혼용해서 사용하기도 하지만 엄연히 차이가 있다. 최적의 가설함수를 찾을때 비용을 측정한다. 데이터셋과 가설의 차이를 비용으로 환산하여 제일 저렴한 비용의 가설을 선택하게 되는데 이때 필요한 용어를 잠시 정리한다.
* Loss Function : ‘특정 데이터 하나’와 '가설함수'의 차이
* Cost Function : ‘데이터셋’과 '가설함수'의 차이(합산)
이전에 Hypothesis를 배웠다. 특징이 하나일때 hθ(x) = θ0 + θ1x 방정식으로 표현할 수 있으며, 이 수식에 θ0, θ1를 대입하여 도식화 하면 선형함수나 다름 없다.
최적의 가설은 어떻게 결정할까 ?
θ는 가설의 형태를 결정짓는 매개변수이므로 θ에 많은 수들을 대입하여 데이터셋에 일치하는 가설함수를 찾아내면된다. case1과 case2중 어떤 가설이 데이터셋과 일치해 보이는가? case2가 상대적으로 더 일치해보일것이다. 데이터셋에 일치하는 가설을 찾는 방법은 ‘가설의 결과’와 ‘데이터의 결과’의 거리가 짧으면된다. 즉, ‘가설의 결과’ - ‘데이터셋 결과’가 최소값이 되면 된다. 다시한번 예를들자면 case1의 '가설-데이터셋'의 거리의 합과 case2의 '가설- 데이터셋의' 거리의 합 중 당연 case2의 합이 작을 것이며 case1 보다 더 적절한 직선이다.
오차의 최소값을 구하려면 θ를 대입한 가설에서 데이터셋의 오차값을 알아야한다. 즉, 이 값이 Cost Function(비용함수)이다.

단변수 선형회귀 가설의 비용함수를 계산해본다.
비용함수의 정의를 순서대로 확인해본다.
- 가설함수 : feature가 1개 이므로 선형함수의 형태의 가설을 표현한다. 편의를 위해 θ0에 0을 대입하여 y절편을 지웠다. (보통 θ0를 포함한다.)

- 오차 제곱 : 단순히 오차를 위해 빼기만 할수 있지만, 차이를 한번더 제곱한다. 이유는 두가지이다. 첫째는 오차의 합을 알아야하기 때문에 음수를 제거하는 작업이고, 두번째는 오차의 값을 늘려서 이후에 가설의 비용을 정확히 측정하기 위해서이다.
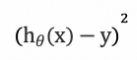
- 오차 제곱 합산 : 모든 데이터와 가설의 오차 제곱을 합산한다. 현재의 가설과 모든 데이터의 차이를 알면 현재의 가설이 얼마나 적합한지 비교할 지표가 된다.

- 평균 제곱 오차 함수 : 오차제곱합산에서 (2*데이터 개수)로 나누어주면 최적의 직선을 찾는 비용함수J가 완성된다. (2로 나눈이유는 경사하강법에서 비용함수를 미분하게되는데 그때 계산의 편의를 위해서다.)

비용함수를 도식화 해보고, 선형회귀의 목적을 생각해본다.
hypothesis의 θ0와 θ1을 다양한 값을 대입하며 여러형태의 직선을 그을수 있었다. 그리고 hypothesis과 데이터셋의 차이, 즉 cost를 알 수 있게됐다. 나아가 cost function이 최소화가 됐을때 최적의 hypothesis가 될것이다. 그래프를 도식화해보며 이류를 살펴보자.
- 가설을 단순화 한다. (θ0, θ1로도 표현하지만 가중치w, 바이어스b로도 표현한다 같은의미이다.)

- 비용함수에 가설을 치환한다.

- 비용함수에 데이터셋을 대입하여 비용 결과를 확인한다.

- 비용을 그래프 상에 표시한다. 점으로 표시된 데이터들의 개수가 무수히 많다면 연속한 함수로 표현될 것이다.

매개변수 θ1(W)의 값이 1일때 가장 작은 비용이므로 매개변수 θ1(W)의 기울기 값이 0일때 최적의 가설이라고 할 수 있다. 비용함수의 도식화가 가능했고, 확인 한 바 그릇모양의 그래프가 그려졌다. 학습알고리즘의 최적화 목표는 비용함수의 값을 최소화 하는 매개변수를 찾는 것이고 이것이 선형회귀의 목적이다.
추후 경사하강법에서 배우겠지만, 위의 비용함수 그래프의 최소값은 W(θ1)의 값이 1일때 이다. 즉, 비용함수의 기울기가 0일때 비용함수는 최소값을 갖는다. 경사하강법에서는 비용함수의 기울기가 0인 W(θ1)를 찾는방법을 배운다.
중간 점검
이제 가설함수, 매개변수, 비용함수, 비용함수 최적화라는 용어들이 조금은 익숙해졌다고 생각한다. 또한 수학적 정의도 어느정도 이해가 됐다. 아니라면 위 글을 한번더 읽어보자.
매개변수가 2개인 가설을 도식화 해본다.
매개변수가 2개인 가설의 비용함수를 도식화하면 3차원 그래프가된다. 바닥면의 x,y축은 θ0, θ1이고, 수직z축은 비용이다. 어렵게 생각할 필요없다. 우리의 목적은 비용함수의 최소화이기 때문이다. 즉, "수직축을 기준으로 가장 아래에 있는 값이 최소 비용함수 값이겠네! " 정도만 이해하고 넘어가면된다.

사람은 다차원 그래프를 이해하는데 한계가 있다. 때문에 등고선 그래프를 사용한다. 중학교 사회과부도 수업에서 산을 표현한 지도를 생각해보자. 높낮이를 타원으로 표현한걸 알수 있다. 그것이 등고선 그래프이다.
- 최적화 되지 않은 비용함수
왼쪽은 가설함수, 오른쪽은 비용함수이다. 가설함수의 비용함수가 오른쪽 발간색x표시의 타원이다. 오른쪽 그래프에서 매개변수 값을 보면 θ0 = 800, θ1 = -0.15이고 즉, 가설은 ‘hθ(x) = 800 + -0.15x’이고 왼쪽 파란선과 일치한다. 데이터셋과 비교해보았을때 파란색선은 적절하지않다. 비용이 비싸다.
- 최적화 된 비용함수
1과 같은 방법으로 왼쪽 파란색 가설 함수를 오른쪽에 표시한다면, 등고선그래프 중앙에 위치할 것이다.
최적의 가설을 찾는 방법을 찾았다. 하지만 귀찮은 작업을 반복해야한다. 등고선 그래프에 점을 찍어가며 수작업으로 비용을 계산하는 것이다. 다음에는 보다 효율적으로 가설함수를 찾는 방법을 소개한다.
참조
머신러닝 코세라 : https://ko.coursera.org/learn/machine-learning
라인하트 브런치 : https://brunch.co.kr/@linecard
'머신러닝' 카테고리의 다른 글
| [머신러닝 이론] 5. Octabe/Matlab 튜토리얼 - 앤드류응 강의 (0) | 2022.05.28 |
|---|---|
| [머신러닝 이론] 4. 다변수 선형회귀 - 앤드류응 강의 (0) | 2022.05.15 |
| [머신러닝 이론] 3. 머신러닝에 필요한 선형대수 복습 - 앤드류응 강의 (0) | 2022.05.15 |
| [머신러닝 이론] 2. 단변수 선형회귀(2) - 앤드류응 강의 (0) | 2022.05.14 |
| [머신러닝 이론] 1. Introdution - 앤드류응 강의 (0) | 2022.05.14 |



